Are you familiar with the term Fourier Analysis and its applications? If not, then this is the perfect place, to begin with, it.
Reputed mathematician Fourier proved in Fourier Analysis that a continuous function can be produced as the infinite sum of the cosine and sine waves.
The results of the analysis made some revolutionary changes in the implications which took place in the synthesis and reproduction of sound in the best way. It is preferably used its science and engineering.
You can also understand Fourier Analysis as a process in which a function is decomposed into different oscillatory components.
Table of Contents
Example of Fourier Analysis
If you want to find out different component frequencies in any musical note then by computing Fourier Transform of any sampled musical note will help you do this.
Any sine wave which is pure will be able to get converted into the sound with the help of a loudspeaker and then can be easily perceived to be a pure and steady tone of a particular single pitch as well.
Some of the areas where this analysis comes in play are-
- Partial differential equations
- Combinatorics
- Number theory
- Signal processing
- Digital image processing
- Probability theory
- Forensics
- Statistics
- Cryptography
- Option pricing
- Acoustics
- Numerical analysis
- Sonar
- Oceanography
- Diffraction
- Optics
- Protein structure analysis
- Geometry and so on
So, now as you are aware of the basics of Fourier Analysis and some of its usages, the time has come to delve into its definition-
Definition of Fourier Analysis
The people need to have a basic understanding of the Fourier analysis to know all about its implications, and we can start from the definition of the analysis, which was proven by Fourier.
To define the Fourier analysis, we can only say that it is basically a process which is used to decompose any particular musical instrument’s sound or more importantly any other particular periodic function which can be then distributed into the constituent cosine and sine waves present in it.
The sound wave can easily be characterized in terms of these amplitudes of the sine waves which are constituent and are responsible for making it up.
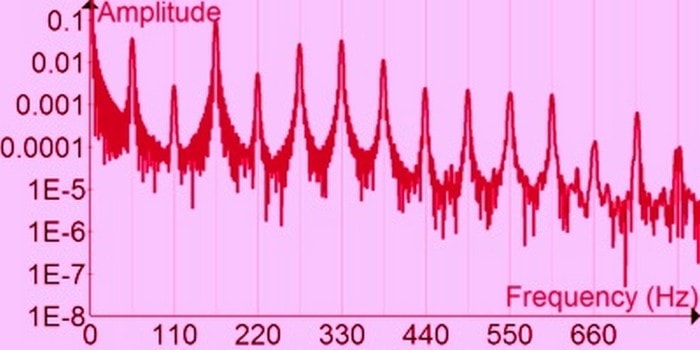
In the image, you can see the Fourier analysis of time signal of open string A note of the bass guitar
So, as the image suggests, Fourier analysis will provide the details about the oscillatory components of functions and signals.
These are the sets of numbers which will be able to tell you all about the certain harmonic content that the sound has, and there is a specific term which is used to refer it, and that is called the Harmonic Spectrum of the sound.
The content which we are referring as harmonic is certainly of great importance because it can be used to determine the timbre of the quality of the musical note, which is sustained in the best way.
Importance of Fourier Analysis
It is also important for people to know all about the meaning of Fourier Analysis to see what it can do in the first place.
Well, this analysis is a particular method which is used to define the periodic waveform in the best way and that too in terms of the basic trigonometric functions such as sine and cosine.
The method has its name from the French mathematician Fourier who was responsible for the analysis in the first place. The method of Fourier analysis has its applications in the fields of electronics, communications, and acoustics too.
There are so many different waveforms which exist, and these waveforms also come with some sort of energy and a proper fundamental frequency. There are some other harmonic frequencies present in these waveforms as well.
The shape that the waveforms would have is determined by a relative proportion of the energy in these harmonics and fundamentals.
What we know as the amplitude of the wave function or frequency can be very easily expressed as the total of the cosine and the sine functions, and that is known as the Fourier series.
This is the series which is defined uniquely with the constants, and these are known as the Fourier coefficients.
Understanding Fourier Analysis
After you are familiar with the harmonic content which is present in the musical sound that is sustained from the Fourier analysis, you will be able to properly synthesize the sound with the help of a particular series which is created with some pure and unique tone generators.
To do that, there should be a compulsory adjustment in the amplitudes as well as the phases. These amplitudes and the phases should be added together as well. That would be known as the Fourier Synthesis.
An important thing that one needs to keep in mind about the sound reproduction that can arise from Fourier analysis is that there is a requirement for a very high-quality reproduction system for the generation of audio.
This system can be used to reproduce the fast transients sounds as well as the percussive sounds too. Let us take the example of a trombone.
There is a sustained sound which is produced from the trombone, and that can be very easily reproduced with a particular range of proper frequencies because sound energy that is produced mostly is in the first few harmonics of their fundamental pitch.
However, in case you want to make sure that you are able to synthesize the cymbal which has a pretty sharp attack properly, it is essential that you need to have a pretty huge range of the higher frequencies which can be used to produce the rapid change in the first place.
One thing that you can do is to visualize this particular task of totalling the sine waves in order to produce the sharp pulses and then you will be able to see that you have to get the larger amplitudes of these waves and that too with the very short times of rises which are also known as the higher frequencies. This will be able to produce the sharp attack of your cymbal properly.
Applications Of Fourier Analysis
There are many different applications of the Fourier Analysis in the field of science, and that is one of the main reasons why people need to know a lot more about it.
Apart from physics, this analysis can be used for the-
- Equalization of audio recordings
- Digital Radio Reception without any superheterodyne circuit
- Image Processing for removing periodic or anisotropic artefacts
- Cross-correlation of same types of images
- X-Ray Crystallography
- Passive Sonar which is used for classifying targets as per machinery noise
- Generation of sound spectrograms and so many other areas where people can benefit from this amazing analysis method.
This applicability of the Fourier analysis comes from the amazing properties that the analysis has. It is essential that the people have an idea about the properties of this method so that they are able to use it in the best way for their purposes.
So, here we are going to provide a list of the amazing properties of the Fourier analysis for the basic understanding of the people-
Key Properties
These transforms are mostly the liner operators, and they can be unitary as well with the help of proper normalization in the best way. This comes from a property which is known as the Parseval’s theorem and also the Plancherel theorem in the general sense.
These are the transforms which are truly and generally invertible, and this is one of the most important things to know about the Fourier analysis properties.
There are some exponential functions which are also the important differentiation functions and these means that the particular representation will transform the linear differential equations that have constant coefficients into some ordinary algebraic options.
So, the behaviour that the linear time-variant system will show is easily analyzed with the help of the frequencies in an independent manner and that too in the best way.
Convolution Theorem and Fourier Analysis
When we talk about the convolution theorem, the Fourier analysis can turn the convolution operation, which is pretty complicated into something that can be considered as a very simple multiplication. So, this is the main thing to notice about these transforms.
With the help of this method, the convolution related operations can be computed in a very efficient and effective manner. The perfect examples of it would be the multiplication of large numbers and the polynomial multiplication.
In the field of forensics, there are some laboratory infrared spectrometers which use this method of Fourier transforms analysis to measure the light wavelengths at which there will be absorption in the infrared spectrum for a particular material.
This is the method which is used to make sure that there is proper decoding of the signals which are recorded and measured along with the data of wavelengths. All you need to do is have a computer, and you are all set.
With the help of this, you will be able to make all the important Fourier calculations and that too in a rapid manner. It will just take a few seconds to complete the entire process in the best way.
Wrapping it up!
The Fourier transform analysis also has its application in the compact and effective representation of any signal. The JPEG compression process actually makes use of the Fourier method to have a digital image in the first place.
Not just that but it also has some applications in signal processing such as radio waves and other types of signals.
So, this is all you need to know about Fourier analysis. We hope this article provided you with the information that you needed.
What according to you are best usages of Fourier Analysis? Share with us in the comments below.